Grouped Data Functions
gd_functions.RmdOverview
This vignette shows an overview of the pipster package
functions for grouped data. Grouped data are consumption expenditure or
income data organized in intervals or bins, such as deciles or
percentiles. In order to estimate poverty and inequality measures from
grouped data, one has to derive a continuous Lorenz curve and use it
together with mean welfare to build a full distribution.
pipster provides a series of functions to estimate poverty
and inequality measures, based on the methodology of Datt
(1998):
pipgd_pov_headcount()(FGT0)pipgd_pov_gap()(FGT1)pipgd_pov_severity()(FGT2)
It also provides a series of functions to calculate distributional measures and to select and validate the best Lorenz curve for subsequent estimation:
Sample Grouped Data
In this vignette, we will explore several typical scenarios in which
the pipster package can be effectively utilized. In each of these
scenario, we will use a sample dataset, pip_gd, available
with the package and obtained from Datt
(1998). The dataset shows the distribution of consumption
expenditure in rural India in 1983. The variables are the following:
- W: Weights, share of population, sum up to 100.
- X: Welfare vector with mean welfare by group.
- P: Cumulative share of population.
- L: Cumulative share of welfare.
- R: Share of welfare, sum up to 1.
#> W X P L R
#> 1 0.92 24.84 0.0092 0.00208 0.002079692
#> 2 2.47 35.80 0.0339 0.01013 0.008047104
#> 3 5.11 45.36 0.0850 0.03122 0.021093739
#> 4 7.90 55.10 0.1640 0.07083 0.039613054
#> 5 9.69 64.92 0.2609 0.12808 0.057248211
#> 6 15.24 77.08 0.4133 0.23498 0.106902117
#> 7 13.64 91.75 0.5497 0.34887 0.113888553
#> 8 16.99 110.64 0.7196 0.51994 0.171066582
#> 9 10.00 134.90 0.8196 0.64270 0.122764156
#> 10 9.78 167.76 0.9174 0.79201 0.149309315
#> 11 3.96 215.48 0.9570 0.86966 0.077653634
#> 12 1.81 261.66 0.9751 0.91277 0.043099829
#> 13 2.49 384.97 1.0000 1.00000 0.087234016Case 1: Simple Welfare Analysis and Lorenz Curve
1.1 Welfare share at a given population share
One simple use case is calculating the welfare share of a specific
share of the population, which can be achieved using
pipgd_welfare_share_at():
# Calculate the welfare share at a given population share
selected_popshare <- 0.5
welfare_share_50 <- pipgd_welfare_share_at(welfare = pip_gd$L,
weight = pip_gd$P,
popshare = selected_popshare,
complete = FALSE)
#> Warning: replacing previous import 'collapse::fdroplevels' by
#> 'data.table::fdroplevels' when loading 'wbpip'When complete = FALSE, the output is a list. The results
can be accessed like so:
# Format the string with the given values
formatted_message <- sprintf("The bottom %.0f%% of the population owns %.0f%% of welfare.",
selected_popshare * 100,
welfare_share_50$dist_stats$welfare_share_at[[1]] * 100)
print(formatted_message)
#> [1] "The bottom 50% of the population owns 31% of welfare."1.2 Quantile share vs cumulative share
pipster has a selection of functions to calculate
welfare shares. When n is declared,
pipgd_quantile_welfare_share() will calculate the share of
welfare owned by a specific share of the population, while
pipgd_welfare_share_at() will return the cumulative
share:
quantile_welfare_share <- pipgd_quantile_welfare_share(welfare = pip_gd$L,
weight = pip_gd$P,
n = 5,
complete = FALSE)
quantile_welfare_share_at <- pipgd_welfare_share_at(welfare = pip_gd$L,
weight = pip_gd$P,
n = 5,
complete = FALSE)
# Combine into a dataframe for practicality
df_combined <- data.frame(
popshare = quantile_welfare_share$dist_stats$popshare,
quantile_share = quantile_welfare_share$dist_stats$quantile_welfare_share,
cumulative_share = quantile_welfare_share_at$dist_stats$welfare_share_at
)
# View the combined dataframe
print(df_combined)
#> popshare quantile_share cumulative_share
#> 1 0.2 0.09067747 0.09067747
#> 2 0.4 0.13345103 0.22412849
#> 3 0.6 0.17201737 0.39614586
#> 4 0.8 0.22138237 0.61752824
#> 5 1.0 0.38247176 1.000000001.3 Estimate and Plot the Lorenz Curve
pister can also be used to estimate a Lorenz curve for a
dataset of grouped data. One hypothetical workflow:
- First, generate the parameters using
pipgd_params() - Validate the parameters using
pipgd_validate_lorenz() - Generate the Lorenz curve using the validated parameters with
pipgd_lorenz_curve()
# Validate Lorenz curve.
parameters <- pipgd_params(welfare = pip_gd$L,
weight = pip_gd$P)
validated_lorenz <- pipgd_validate_lorenz(params = parameters,
complete = TRUE)
# Select the best Lorenz curve and check which method has been used.
selected_lorenz <- pipgd_select_lorenz(params = validated_lorenz)
lorenz_used_for_dist <- selected_lorenz$selected_lorenz$for_dist
lorenz_used_for_pov <- selected_lorenz$selected_lorenz$for_pov
formatted_message <- sprintf("%s used for distribution statistics and %s used for poverty metrics.",
lorenz_used_for_dist,
lorenz_used_for_pov)
print(formatted_message)
#> [1] "lq used for distribution statistics and lb used for poverty metrics."
# Plot the Lorenz Curve
lorenz_curve_data <- pipgd_lorenz_curve(params = validated_lorenz)
plot(lorenz_curve_data$lorenz_curve$points,
lorenz_curve_data$lorenz_curve$output,
type = 'l', col = 'blue',
xlab = 'Cumulative Share of Population',
ylab = 'Cumulative Share of Welfare',
main = 'Lorenz Curve',
xlim = c(0, 1), ylim = c(0, 1),
xaxs = "i", yaxs = "i")
# Add the line of equality
abline(0, 1, col = 'red', lty = 2)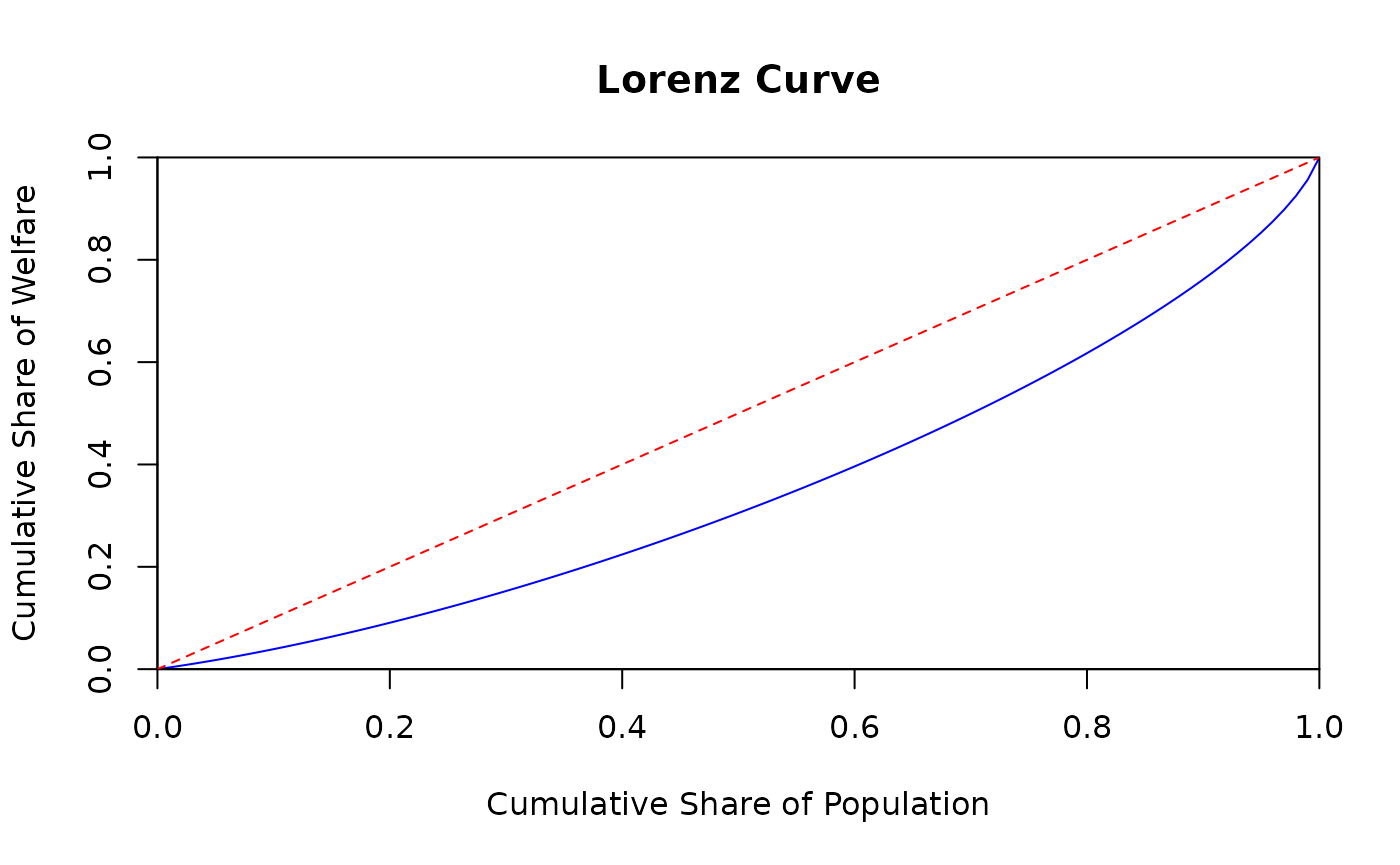
Case 2: Poverty Profiling Manual vs Pipster
pipster allows the user to estimate poverty measures
quickly and accurately using the Lorenz curve. To demonstrate its use,
we can manually calculate FGT(0), FGT(1), and FGT(2), and then replicate
it using only pipster functions.
2.0 Manual parameters
Following Datt(1998), we first derive the necessary parameters from
the Lorenz curve using pipgd_lorenz_curve():
# STEP 0 : assign variables
cum_welfare <- pip_gd$L
cum_pop <- pip_gd$P
# STEP 1: Estimate Lorenz Curve
lorenz_curve_params <- pipgd_lorenz_curve(welfare = cum_welfare,
weight = cum_pop,
complete = TRUE)
print(lorenz_curve_params$selected_lorenz$for_pov)
#> [1] "lb"pipster suggests to use lb, the Lorenz
beta, for poverty measures estimation. We will use lq
instead to compare our results with the ones reported in the article. We
then retrieve the parameters and assign them to objects:
# parameters
m <- lorenz_curve_params$gd_params$lq$key_values$m
n <- lorenz_curve_params$gd_params$lq$key_values$n
r <- lorenz_curve_params$gd_params$lq$key_values$r
s1 <- lorenz_curve_params$gd_params$lq$key_values$s1
s2 <- lorenz_curve_params$gd_params$lq$key_values$s2
a <- lorenz_curve_params$gd_params$lq$reg_results$coef[[1]]
b <- lorenz_curve_params$gd_params$lq$reg_results$coef[[2]]
c <- lorenz_curve_params$gd_params$lq$reg_results$coef[[3]]
z <- 89 # the poverty line for rural India, 1983.
mu <- 109.9 # the actual mean of the sample.
# helpful combinations
z_div_mu <- z/mu
mu_div_z <- mu/z2.1 Poverty Headcount
In pipster, we can apply the
pipgd_pov_headcount() function to determine the proportion
of the population living below a specified poverty line. The poverty
headcount can be calculated manually as follows:
\[H=-\frac{1}{2 m}\left[n+r(b+2 (z / \mu))\left\{(b+2 (z / \mu))^2-m\right\}^{-1 / 2}\right]\] Manually:
H <- -(1/(2*m)) * (n + r*(b + 2*(z_div_mu)) * ((b + 2*z_div_mu)^2 - m)^(-1/2))
print(paste0("The poverty headcount is ", round(H*100,2), "%"))
#> [1] "The poverty headcount is 45.06%"Using pipster, we simply do:
headcount1 <- pipgd_pov_headcount(welfare = pip_gd$L,
weight = pip_gd$P,
mean = mu,
povline = z,
lorenz = 'lq')
print((paste0("The poverty headcount is ", round(headcount1$headcount*100,2), "%")))
#> [1] "The poverty headcount is 45.06%"One might want to calculate the poverty line using
povertyline = mean * times_mean instead. When defining
these parameters, it is important not to define a poverty line as well,
otherwise the parameter times_mean will be ignored:
headcount2 <- pipgd_pov_headcount(welfare = pip_gd$L,
weight = pip_gd$P,
mean = mu,
times_mean = 0.8,
lorenz = 'lq')
print(headcount2)
#> povline headcount lorenz
#> <num> <num> <char>
#> 1: 87.92 0.4403688 lq2.2 Poverty Gap
Next, we use the pipgd_pov_gap() function to calculate
the poverty gap index. This index measures the average shortfall of the
population from the poverty line, expressed as a percentage of the
poverty line. It can be calculated as follows:
\[PG = H - (\mu / z) L(H)\] Manually:
# First we calculate the value of the Lorenz curve at H:
L_at_H <- pipgd_welfare_share_at(welfare = cum_welfare,
weight = cum_pop,
popshare = H)$dist_stats$welfare_share_at
# Then we calculate the poverty gap:
PG = H - mu_div_z*L_at_H
print(paste0("The poverty gap is ", round(PG*100,2), "%"))
#> [1] "The poverty gap is 12.47%"Using pipster, we simply do:
gap <- pipgd_pov_gap(welfare = pip_gd$L,
weight = pip_gd$P,
mean = mu,
povline = z,
lorenz = 'lq')
print((paste0("The poverty gap is ", round(gap$pov_gap*100,2), "%")))
#> [1] "The poverty gap is 12.47%"2.3 Poverty Severity
Finally, we utilize the pipgd_pov_severity() function to
assess the poverty severity index. This index considers the squared
poverty gap, placing more weight on the welfare of the poorest. It can
be calculated as follows:
\[\begin{aligned} & P_2=2(P G)-H \\ & -\left(\frac{\mu}{z}\right)^2\left[a H+b L(H)-\left(\frac{r}{16}\right) \ln \left(\frac{1-H / s_1}{1-H / s_2}\right)\right] \end{aligned}\]
SPG = 2*PG - H - ((mu_div_z)^2) * (a*H + b*L_at_H - (r/16) * log((1-(H/s1))/(1-(H/s2))))
print(paste0("The poverty severity is ", round(SPG*100,2), "%"))
#> [1] "The poverty severity is 4.75%"Using pipster, we simply do:
severity <- pipgd_pov_severity(welfare = pip_gd$L,
weight = pip_gd$P,
mean = mu,
povline = z,
lorenz = 'lq')
print((paste0("The poverty severity is ", round(severity$pov_severity*100,2), "%")))
#> [1] "The poverty severity is 4.75%"Case 3: Additional Inequality and Poverty Measures
Finally, pipster can also be used to easily calculate
additional inequality measures. The Gini coefficient can be calculated
using pipgd_gini() like so:
gini <- pipgd_gini(welfare = pip_gd$L,
weight = pip_gd$P,
lorenz = 'lq')
print((paste0("The gini index is ", round(gini$dist_stats$gini,2))))
#> [1] "The gini index is 0.29"The Watts Index can be calculated using pipgd_watts()
like so:
watts <- pipgd_watts(welfare = pip_gd$L,
weight = pip_gd$P,
mean = mu,
povline = z,
lorenz = 'lq')
print((paste0("The Watts index is ", round(watts$watts, 2))))
#> [1] "The Watts index is 0.43"And finally, the MLD (Mean Logarithmic Deviation) can be calculated
using pipgd_mld() like so: